Tag Archives: how to

Making explainer videos for your software

If you want to find out how to do something, such as do a mail merge in Word or fix a leaky valve on a radiator, where do you look first? Probably Youtube. Videos are an excellent way to explain something. More bandwidth than text and more scaleable than a 1-to-1 demo.

I’ve done explainer videos for all 3 of my products. But I found it a real struggle. I would write a script and then try to read the script and do the screencast at the same time and do it all in one take. I would stutter and stumble and it would take multiple attempts. It took ages and results were passable at best. I got some better software to edit the stumbles out, so I didn’t have to do it in one go. But it still took me a fair few attempts and quite a bit of editing. It became one of my least favourite things to do and so I did less and less of it.

Recently, I came across these slides on video by Christian Genco. These and subsequent Twitter exchanges with Christian convinced me that I should stop being a perfectionist about video and just start cranking them out on the grounds that a ‘good enough’ video is better than no video at all (‘the perfect is the enemy of the good’) and I would get better at it over time. As Stalin supposedly said “Quantity has a quality all of it’s own”.

So I have ditched the scripts and the perfectionism and I’ve managed to create 13 short Easy Data Transform explainer videos in the last week or so. And I am getting faster at it and (hopefully) a bit more polished. I’m definitely not an expert on this (and probably never will be) but here are some tips I have picked up along the way:

Get some decent software. I use Camtasia on Windows and it seems pretty good.

Try to talk slower.
Try to sound upbeat (not easy if you are British and could voice double for Eeyore).
Try not to move the mouse and talk at the same time. This makes editing a lot easier. Some people like to do the audio and the visual separately, but that seems like too much hassle.
If you stumble, just take a deep breath, say it again and then edit the stumble out later.
Get a reasonable mic. I have a snowball mic on a cantilevered stand. I covered it with a thin cloth to try to reduce pops.
The occasional ‘um’ is fine.
Have a checklist of things to do for each video, so you don’t forget anything (such as disabling your phrase expander software or muting the phone).

My setup. Note the high tech use of rubber bands.

I’m lucky to have a very quiet office, so I don’t have much background noise to contend with.

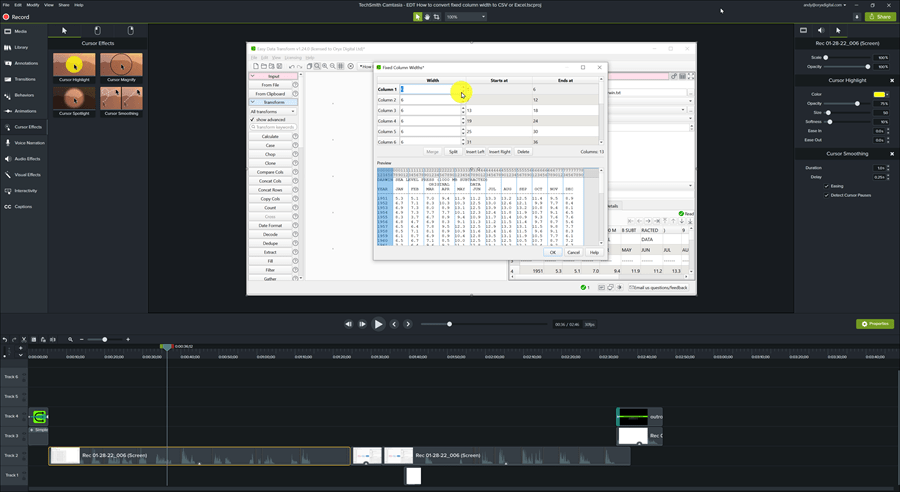
Using Camtasia I can easily add intos and outros, edit out stumbles and add various effects, such a mouse position highlighting and movement smoothing. I just File>Save as the previous project so that I don’t have to re-add the intro and outro. Unsurprisingly, Camtasia have lots of explainer videos. I wish there was a way to automatically ‘ripple delete’ any sections where there is no audio and no mouse movement (if there is, I haven’t found it). Some people recommend descript.com. It looks interesting, but I haven’t tried it.

I did an A/B test of recordings with my Senheiser headset mic against my Snowball mic and the consensus was that the headset was ok but the the Snowball mic sound quality was better.

Some people prefer to use synthetic voices, instead of their own voice. While these synthetic voices have improved a lot, they never sound quite right to me. Also it must be time consuming to type out all the text. Or you can pay to have a professional voiceover done, but this is surprisingly expensive (around $100 per minute, last time I checked) and almost certainly more time consuming than doing it yourself.

Some people aren’t confident about speaking on videos because they are not native speakers of that language and have an accent. Personally accents don’t bother me at all. In fact I like hearing English spoken with a foreign accent, as long as I can understand it. Also I think there is an authenticity to hearing a creator talk about their product in their own voice.

I’m not a big fan of music on explainer videos, so I don’t add any.

I let Youtube generate automatic captions for people that want them (which could be people in busy offices and on trains and planes, as well as the hearing impaired). They aren’t perfect, but they are good enough.

My videos are aimed at least as much at finding new users as helping existing users. So I make sure I research keyword terms (mostly in Google Adwords) before I decide which videos to make and what to title them. Currently I am targetting very specific keyword searches, such as How to convert CSV to Markdown. Easy Data Transform can do a lot more than just format conversion, but from an SEO point of view it is better to target the phrases that people are actually searching for.

I upload the videos as 1080P (1920 x 1080 pixels) on to the Easy Data Transform Youtube channel and onto my screencast.com account (which I pay a yearly fee for). I then embed the screencast.com videos on relevant easydatatransform.com pages using IFRAME embed codes created by screencast.com. I don’t use the Youtube videos on my website, because I don’t want people to be distracted by Youtube ads and ‘you may also like’ recommendations. They might be showing a competitor! I don’t host the videos on the website itsself as I worry that might slow down the website. I also link to the videos in screencast.com from my help documentation, as appropriate.

Some people like to embed video of themselves in screencasts, in the hope of making it more engaging. But personally I want people to concentrate on my software, rather than being distracted by the horror of my face. And not having to comb my hair or look smart was part of what got me into running my own software business.

In the next few months I will be checking my analytics to see how many views these videos get and whether they increase the time on page and reduce the bounce rate.

If you can spare a few seconds to go to my Youtube page and ‘like’ a video ot two or subscribe, that would be a big help!

Note that some of the above doesn’t apply when you are creating a demo video for your home page, rather than an explainer video. Your main demo video should be slick and polished.

How to make difficult decisions

When you run a business (even a small business like mine) you have to make a lot of decisions. Many of these decisions are complicated and have to be taken with incomplete information. But you can’t take too long over them, or you will never get anything done. Here are 3 techniques I use to help with difficult decisions.

Break it down

This is a very simple method for breaking a difficult decision down into smaller parts using a spreadsheet.

Decide the criteria that are important for the decision. Add a row for each.
Add a weighting column. Assign each criteria a weighting in the range 1 to 10, depending on its relative importance to you.
Add a column for each option you are considering.
Set each criterion/option cell a value in the range 0 to 10, depending on the extent to which the choice for that column fulfils the criteria for that row.
Calculate the weighted sum for each column.
Choose the outcome with the highest weighted sum.

Here is an example for choosing between 3 different types of hosting:

It’s not particularly scientific, but it does force you to systematically break down the problem into smaller parts and justify your decision.

Take the long view

It sometimes helps to stand back and look at the bigger picture. I can think of no better way to do that than to ask a hypothetical (hopefully elderly) future me, lying on my deathbed, which option they approve of. For example, given the choice between adding an innovative new feature to my product or improving the conversion funnel by a few percent, I think future me would be happier that I chose to add the innovative new feature. It is also a useful reminder that many decisions probably aren’t all that important in the grand scheme of things.

Flip a coin

Sometimes you need to make a decision, but you don’t have enough information or the time taken to get that information is going to cost you more than making the wrong decision. In that case, don’t agonise over it. Just roll a dice or flip a coin and move on.

Pivot Tables demystified

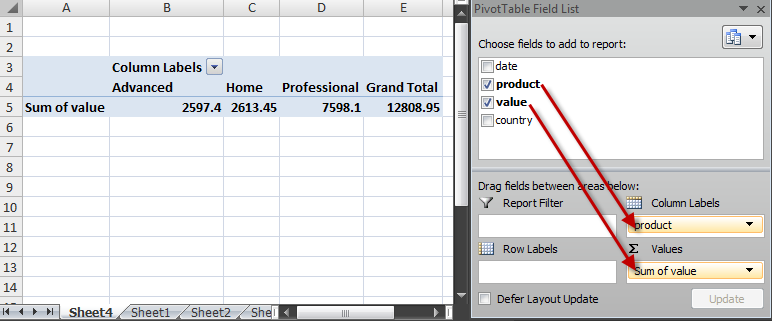
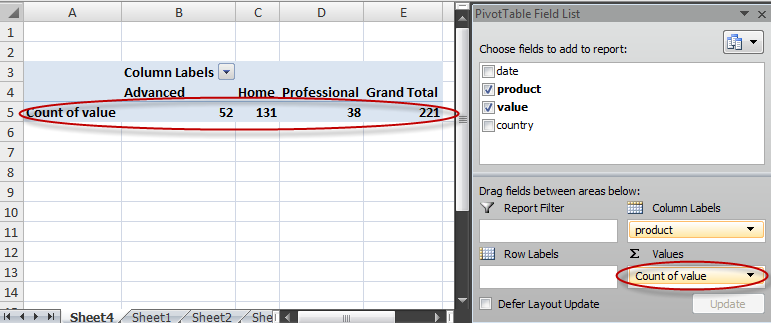
Online businesses generate a lot of data. Sales data, marketing data, traffic data etc. Pivot tables can be a useful tool for analysing and extracting useful information from this sea of data. A lot of people seem to have heard of Pivot Tables without understanding what they are or how to use them. Despite the slightly cryptic name they are really just a way of summarizing tables of data. Nothing to be intimidated by. I’m going to try to demystify them here with a simple example.

Let’s imagine you have got an Excel spreadsheet with a month of (fictitious) sales transaction. It looks like this:

You want to find out:

The total value of sales of each product
The number of sales of each product
The total value of sales of each product by country
The total value of sales of each product by day of the week

How would you do it? You can crunch the numbers using a calculator, but that is very tedious and error prone. If you are a programmer you can export the data to a .csv file and write a small program in your favourite language to read it in, crunch the data and write the results out. You probably think you can do it in 10 minutes, but I bet it will take you at least an hour to get it working and debugged. I did all the above in 1 minute and 20 seconds using Excel pivot tables.

Here is how you can do it (screenshots from Excel 2007). You can download the spreadsheet if you want to try it yourself.

Select all the data, including the header (A1 to D222).

Click on Insert in the Excel Ribbon bar.

Click on PivotTable.

The Create Pivot Table window will appear. Click OK.

The PivotTable Field List will appear. We want to find the number of sales for each product. Drag the product field to Column labels and the value field to Values. This gives us the total value of sales by product.

To change this to the number of sales pull down the Sum of value drop-down list and select Value Field Settings….

Change Summarize value field by from Sum to Count and click OK.

The number of sales of each product are now shown.

Now drag the country field to Row labels. Then click on Count of value, select Value Field Settings…, change it back to Sum and click OK. The total value of sales of each product by country is now displayed.

We now need to add a day of the week column. Click on Sheet 1 and add a new column as shown.

Now select all the data from A1 to E222 and insert a new pivot table, as before.

Drag the fields as shown to get the total value of sales of each product by day of the week.

(We’ll quietly ignore the fact that the number of days aren’t divisible by 7 in the data.)

We can even display by product, day of the week and country with one more drag.

Excel also supports pivot charts if you prefer your results in graphical form.

Obviously this is a very simple example, but pivot tables can be used to quickly analyse much larger and more complex data sets. Next time you have got some data to analyse consider whether you would be better using pivot tables or pivot charts.

*** UPDATE ***

You can also use my Hyper Plan software to create pivot tables. It is a lot simpler than the above! There is a free trial.

How to build an igloo

We have had loads of snow here in the UK. Loads by UK standards anyway (I don’t think a Scandinavian would be very impressed). So I decided to take full advantage of the flexibility my job allows and build an igloo. It was my second attempt and it turned out much better than rather wonky one I did a few days ago. This post is a quick overview of the modest amount I have learnt about igloo building, in case you are inspired to build your own.

First of all, building materials. The snow needs to be the sort you can squash together to make a snowball. If it is too powdery to stick together, forget it – you won’t be able to make a worthwhile igloo. Try again tomorrow.

Next you need to mark a circular base for your igloo. If you don’t then it is hard to get a decent overall shape. Two twigs and a bit a string is all you need to draw a circular outline. Don’t be too ambitous though, it takes a surpising amount of snow to build an igloo and the amount goes up fast as you increase the diameter. 1.5 to 2 metres diameter is plenty for a first attempt.

Then you need to have a bucket-shaped receptacles in a range of sizes. I used a household bucket as the largest, 2 different sizes of flower pot and a child’s bucket as the smallest. Start with the largest receptacle. Use it as a mould to create ‘snow bricks’. Pack the snow into the mould tightly to make strong bricks. Lay a circle of these bricks as close together as possible, leaving a gap for the door. Then place the next layer of bricks on top, interleaving them like standard brickwork. Pack the gaps between the bricks with loose snow like mortar in brickwork.

Every few layers you need to swap to a smaller mould. Each layer needs to curve inward a bit more than the previous one to form the dome. It is quite surprising how easy it is to build an arch out of snow. It is stronger and stickier than you might think.

It took 3 adults a couple of hours to complete the igloo. I don’t think the Inuit will be offering us a job anytime soon, but it was very satisfying. Considerably more satisfying than the several hours I spent this morning failing to work out how to get rid of a maximise icon in Mac OS X.

A YouTube video of a similar approach using stacking boxes